Even for experienced options traders, understanding the relationship between how an option changes in price and how its underlying stock changes price can be difficult. To make prediction easier, traders turn to a set of variables – vega, delta, gamma, theta, and rho – collectively known as the “Greeks.” The Greeks relate an option’s price to measurable factors related to the underlying stock and market, such as stock price and volatility and interest rates. These variables are essential for predicting how an option’s price may change in response to changes in a stock’s price or in the broader market.
Using “Greeks” for Options Trading
Even among options traders, choosing to use the Greeks to inform trading is not a given. Although they can provide valuable information, they also add a layer of complexity that can muddle options trading. Most important, they can distract from the most important component affecting the value of an options position, which is the difference between the stock price and strike price and the value decay with decreasing time to expiration on the option itself. For these reasons, several famous options traders, such as John Carter, hardly study the Greeks at all when making trades. When determining whether to use the Greeks, consider your strategy for options positions and be sure to not lose sight of the time-driven value of options.
The Greeks in Brief
Before diving into each Greek variable in detail, it can be helpful to have an overview of what each aim to describe. In brief, vega measures the sensitivity of an option’s price to changes in how volatile the underlying stock’s price is. Delta measures how sensitive an option’s price is to changes in the underlying stock’s price, while gamma measures the rate of change of delta. Theta accounts for the value decay in an option as it approaches its expiration date. Finally, rho indicates how an option’s price will change given a change in prevailing interest rates.
Vega
Vega measures how sensitive an option’s price is in relationship to how volatile the underlying stock’s price is. Importantly, the volatility accounted for is the expected volatility over the timespan of the option rather than the stock’s historical volatility. Typically, option prices are expected to increase or fall by the amount of vega for each 1% increase or decrease, respectively, in a stock price’s volatility. In addition, the sign of vega depends on whether an option is long or short – both long calls and puts have positive vega values, while both short calls and puts have negative vega values. Vega can be difficult to understand for beginner options traders, but is especially important because it can cause an option’s value to fall even as a stock’s price is rising if the volatility decreases at the same time.
Delta
Delta measures how an option’s price will change in response to a $1.00 change in the underlying stock price. The value of delta is relatively straightforward to understand and is influenced by an option’s time to expiration and the difference between the option’s strike price and the underlying stock’s price. As an example, a call option for Apple, whose stock price is currently at, say, $175, and has a delta value of 0.4 indicates that if Apple’s stock price moves to $180, the option price will increase by $2.00 (0.4 times $5.00).
A common use of delta is to determine whether an option is likely to expire in the money. An option’s likelihood of expiring in the money is equivalent to delta for both in the money and out of the money calls. Thus, options with higher delta values are more likely to expire in the money – and for this reason are often more expensive.
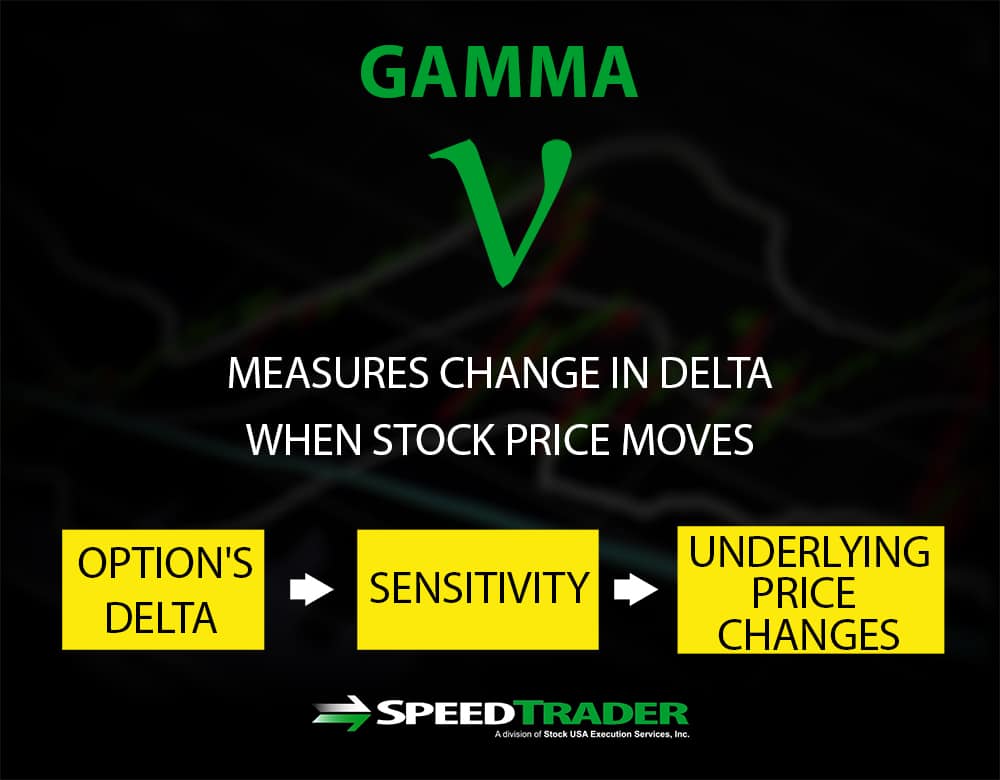
Gamma
Delta isn’t static – it changes as an option approaches expiration and as the underlying stock price changes. The Greek variable gamma indicates the rate of change in delta for each one-point change increase in the underlying stock’s price. In effect, gamma can be thought of as a measure of how volatile an option’s price may be in response to changes in the underlying stock’s price. Where delta represents the probability of an option expiring in the money, gamma represents the stability of that probability over time such that a lower gamma indicates a more stable delta.
Theta
Theta accounts for the value decay in an option as it approaches its expiration date – the value of an option decreases by the amount of theta each day. In essence, theta measures how much value an option loses while the option holder considers whether to exercise it. Theta can be relatively gentle in slope over the life of an option, but can also spike dramatically as an option approaches expiration. Typically, theta is smaller for options in the money than options that are at or out of the money.
Rho
Rho measures how much the price of an option should rise of fall for a 1% change in the prevailing interest rate. This variable is typically not an important consideration unless it is expected that the interest rate may change during the timespan of an option. When the interest rate does change, an increased rate typically pushes up the price of call options and pushes down the price of put options. For this reason, higher interest rates result in call and put options whose strike prices are equivalently far from the underlying stock price to diverge more in price.
How Do the Greeks Work Together?
In real-world trading, the five individual Greek variables are all changing simultaneously and propagate their changes through the other variables. The result is significant complexity, since any change in the underlying stock’s price, interest rates, or time to expiration can influence all of the variables in ways that require a computer model to fully calculate. However, understanding how and why each individual Greek variable moves can help to make sense of what will happen to an option’s price as changes occur.
The Black-Scholes Model
The Black-Scholes model is one of the most widely used equations for determining the fair price of an option, and it accounts for many of the same factors that the Greeks attempt to represent. The model uses five variables to calculate an option’s price: the strike price, the underlying stock price, the time to expiration, the interest rate, and the volatility of the underlying stock. The model makes several assumptions, such as a constant interest rate and constant volatility over the option’s life, that may not hold true in some cases. In addition, the fair price calculated is for European rather than American options, since the model assumes that options cannot be exercised before their expiration date.
Summary
The price of an option does not trend in a linear fashion with the price of its underlying stock. Instead, it depends on a variety of additional factors, including the stock’s volatility, the strike price and time to expiration of the option itself, and the prevailing interest rate. Vega, delta, gamma, theta, and rho – collectively referred to as the Greeks – provide information about specifically how an option’s price will react to changes in these factors. However, the Greeks are constantly changing in value and the value of one Greek affects the value of all of the others. Thus, computer models based on these variables are typically required to fully understand how an option’s price will change.